Results

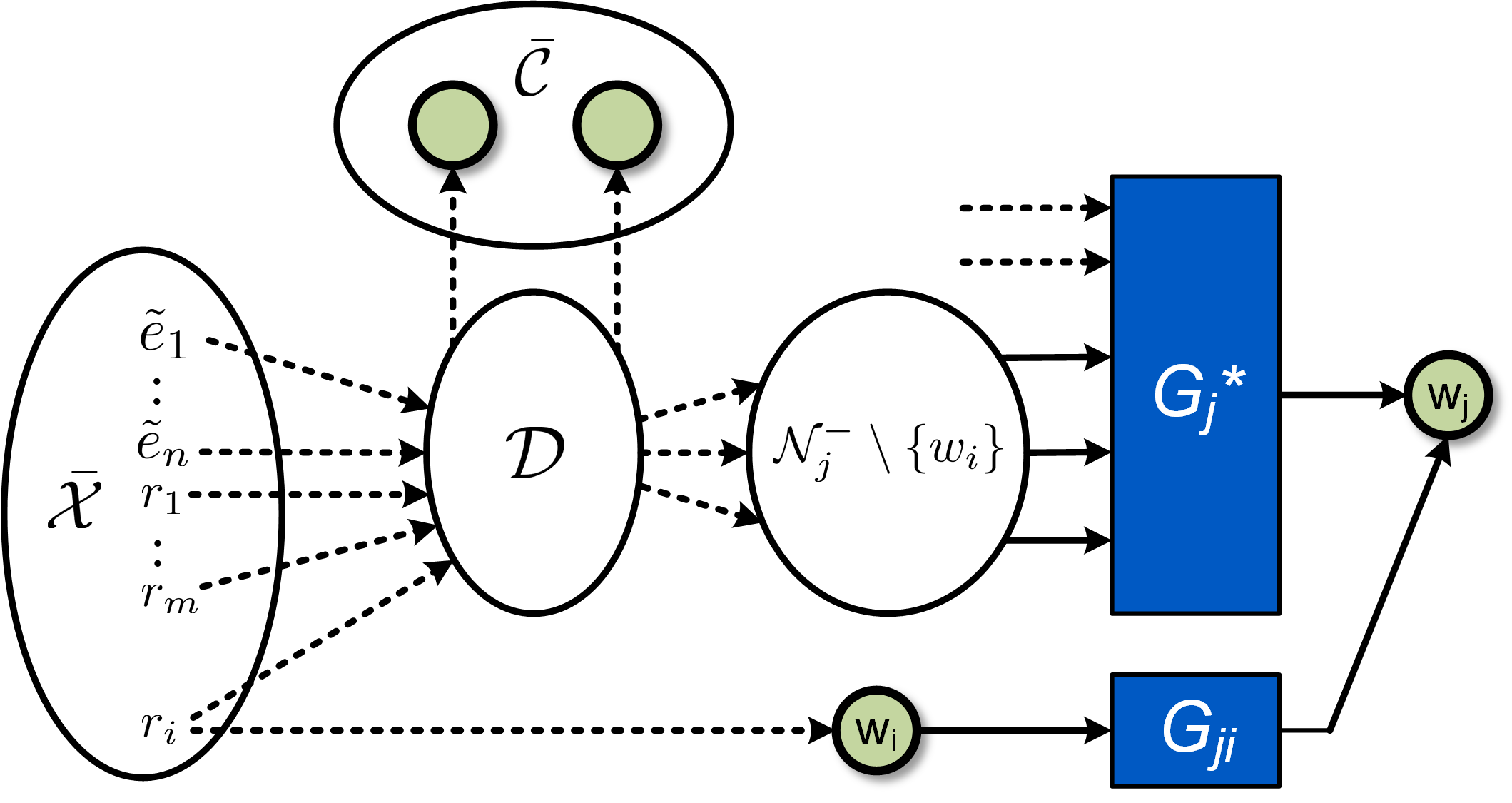
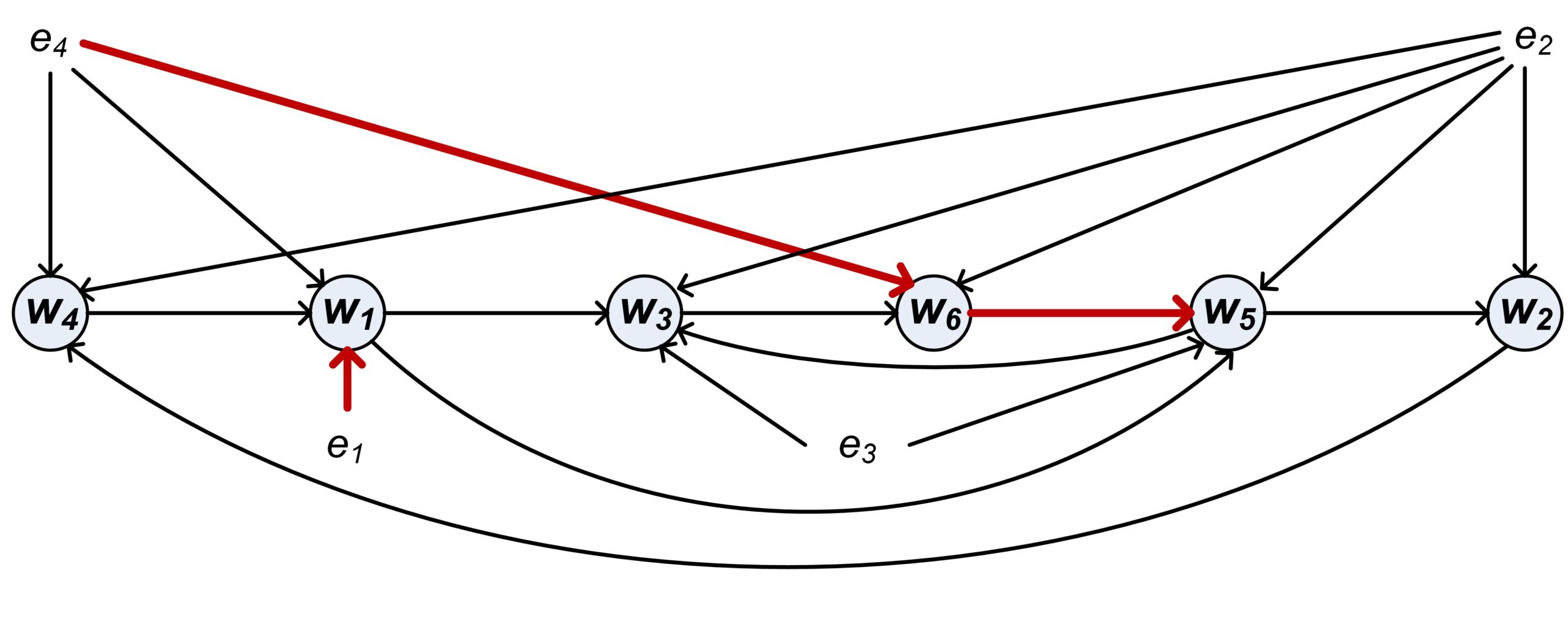
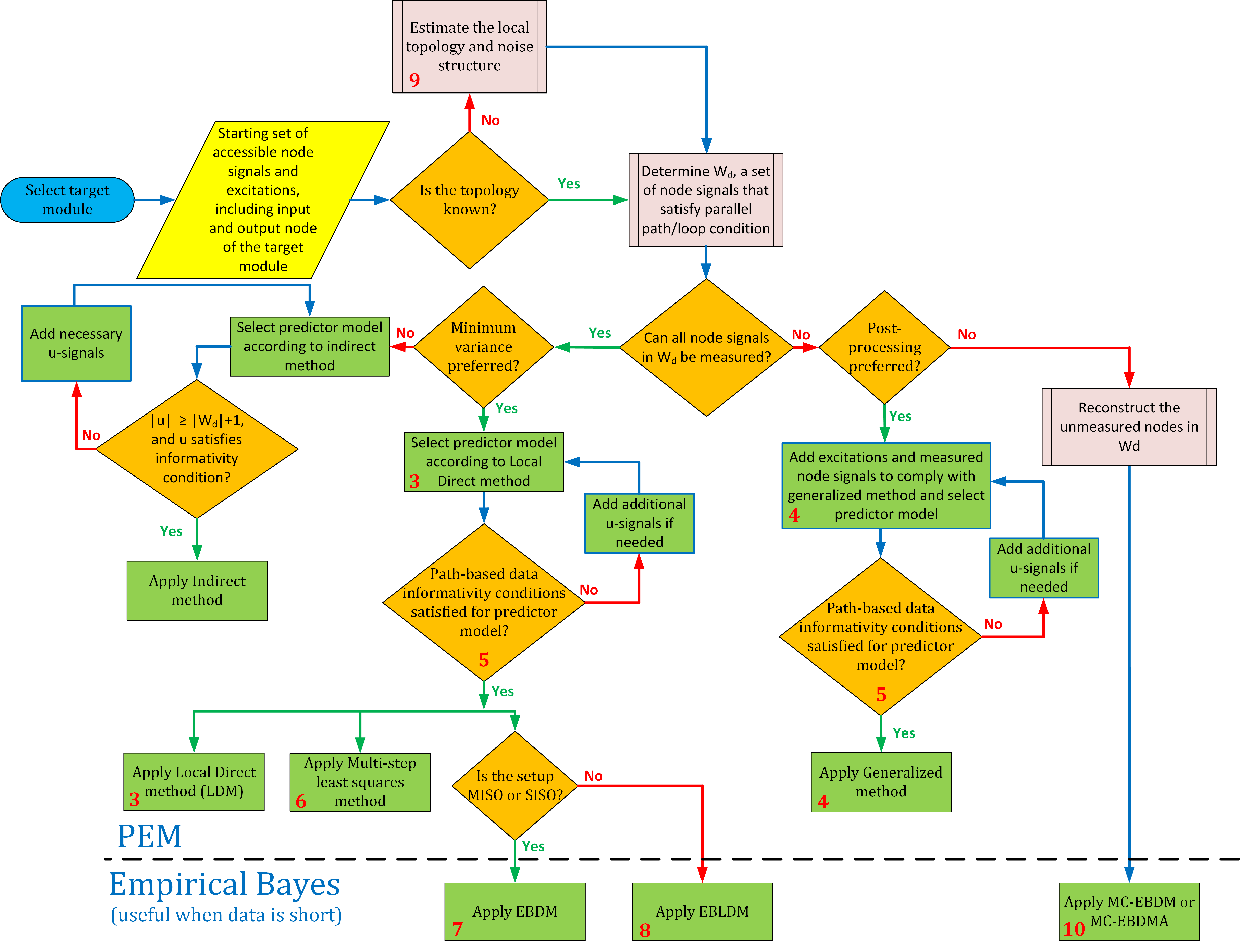
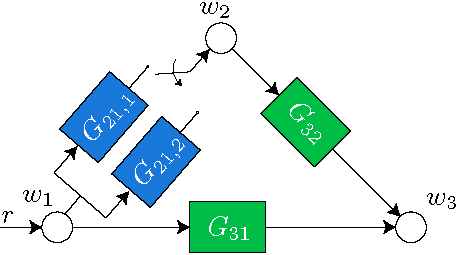
Modelling dynamic networks

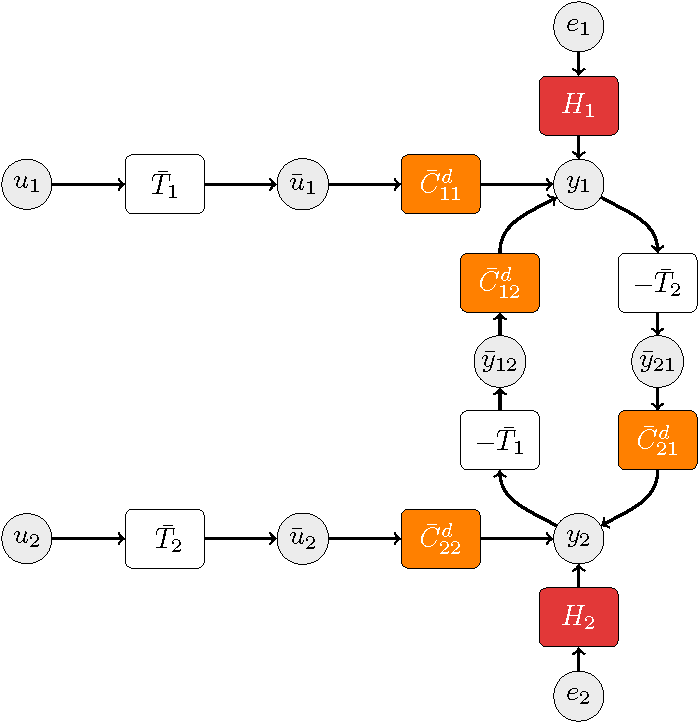
There are many different ways of representing interconnected dynamic systems. The format that we have chosen to use as a basis for our developments is the so-called module-framework, where linear dynamic systems are represented by transfer functions (modules) that are interconnected through signals, which are interconnected through summation points.  External signals affect the network in the form of (measured) excitation/probing signals and (unmeasured) disturbance signals. The topological properties of the network are characterized by a graph, in which the signals are represented as nodes, and the modules are (directed) links between the nodes.

The network is slightly different from the often used state-representation of a dynamic network. This is motivated by our focus on data-driven modeling problems. Since in a large-scale system typically not all states can be measured, we have chosen for a framework where the node signals could be considered as those states that can possibly be measured. States that can not be measured are “hidden” in the dynamic transfer functions in the models.

The module representation has been introduced in Van den Hof et al. (2013) and has been adopted by several other research groups in this domain.
Relations between module and state-space representations have been explored in Kivits and Van den Hof  (IFAC SYSYS 2018).

Diffusively coupled networks

Physical systems are often characterized by network representations with a particular type of couplings, referred to as diffusive couplings, meaning that an effect occuring between two nodes is dependent on the difference between the node variables. Think of a current that flows on a link as a results of a voltage difference between nodes. These physical networks are characterized by a non-directed graph where all links between nodes have some symmetry properties. Identification methods for these physical networks have been developed in Kivits et al. (CDC-2019 and IEEE Trans. Autom. Control 2023) for the situation of full rank disturbances. It has appeared that for the handling of these diffusively coupled networks, polynomial model representations are more attractive than the transfer function representation that are used in the module framework. The prime argument for this is that the structural symmetry properties of the networks are directly apparent in the chosen polynomial form.

The identification of a single interconnection / component in a diffusively coupled network has also been addressed in a similar prediction error framework, see Kivits and Van den Hof (IEEE CDC 2022). It has been shown that in the situation of a single interconnection, it suffices to measure the node signals that form the single interconnection, and in addition all node signals that are direct neighbours of the first two. This shows that a local identification problem can indeed be kept local in terms of the required measured node signals.

Network identifiability

Network identifiability is a property that determines whether different network models can be distinguished from each other on the basis of measured data. It is typically applied to network models with a given topology, and dependent on the following aspects:

• The presence and location of measured external excitation signals
• The presence, location and correlation structure of disturbance signals
• The presence of a priori known modules with fixed dynamics

Network identifiabilty has been defined and analyzed in Weerts et al. (Automatica, March 2018; PhD-Thesis, 2018). It is a necessary property for arriving at a consistent estimate of the network dynamics. A synthesis algorithm for allocating external excitation signals to achieve (generic) network identifiability is presented in Cheng et al., (IEEE-TAC, 2022). It is fully graph-based and determines the location of external excitation signals, for the situation that all node signals are measured, on the basis of a pseudo-tree covering of the network graph.
The algorithm has been extended to also effectively deal with modules in the network that are known/fixed a priori, see Dreef et al., (IEEE LCSS 2022).

Single module identifiability

When focusing on the determination of a single module in the dynamic network, network identifiability can be restricted to apply to this single target module only. The resulting question then is: where to excite the network and which node signals to measure in order to arrive at identifiability of the target module. The question is most attractively addressed in a generic sense, leading to analysis and synthesis algorithms that are based on the network graph only.

This problem is addressed in Weerts et al. (CDC 2018) and Shi et al. (IFAC 2020, Automatica 2022) for the situation of full measurement of all node signals, and in Shi et al. (IEEE Trans. Autom. Control 2023) for the situation of partial measurement and partial excitation.

Full network identification

Using standard (prediction error) methods for full network identification will most often lead to non-convex optimization problems that become unpractical in terms of computational complexity and the lack of guarantees of reaching global optima. This particularly holds true if the networks become increasingly complex in terms of the number of nodes involved. Therefore alternative methods have been developed that restrict to computational attractive steps most often relying on convex optimizations. In a teamwork between researchers from KTH Stockholm and TU Eindhoven, a sequential least squares method has been developed for identifying dynamic networks in ARMAX form, for the situation of full rank disturbances (Weerts et al., IFAC SYSID 2018).  A follow up was made in terms of a multi-step algorithm, exploiting the so-called weighted nullspace fitting reasoning, in Fonken, Ramaswamy and Van den Hof (Automatica, 2022), where the step was made to include estimation of the noise rank and noise topology within the algorithm.

Identification methods for single module identification

If the objective is to identify a single module in a dynamic network, one of the prime questions is: which node signals need to be measured to allow for the accurate estimation of this target module.  This choice is typically reflected in the construction of the predictor model, i.e. the sets of inputs and outputs that are being considered in the estimation problem.

A first choice in identification method typically is the choice between a direct and an indirect method, similar to the situation of a (classical) closed-loop identification problem. In indirect methods, first models of closed loop transfer functions are being estimated, after which through postprocessing these results, an estimate of the target module is obtained. Indirect methods typically impose relatively strong conditions on the presence of external excitation signals.

In the SYSDYNET project the “local direct method” has been developed for direct identification of a target module, under the condition that the network topology is known. This method can optimally exploit excitation through non-measured disturbance signals, thus imposing less strong conditions on measurable external excitation signals in the network, and satisfies maximum likelihood properties in the setting of prediction error identification methods.

The selection of predictor model inputs and outputs is a very “rich” problem, with non-unique solutions. Conditions that typically need to be satisfied include:

• A graphic “parallel path and loop condition” that avoids bias in the estimates;
• Graphic conditions for dealing with confounding variables;
• Conditions on data-informativity.

The method is presented in Ramaswamy et al. (IEEE TAC 2021) while graph-based data-informativity conditions are presented in Van den Hof et al. (Proc. CDC 2020).

Handling confounding variables in network identification problems

Confounding variables are unmeasured node signals (e.g., disturbances) that affect both the input and output of the predictor model, and therefore create correlation between these signals that is not induced by the dynamics of the network modules. It is a typical handicap in statistics. In the system identification domain there actually exists a very effective way to deal with these confounding variables, by modelling them as correlated disturbances in a multivariate disturbance model. The consequence of using this approach is that in our predictor models, input node signals that share a confounding variable with one of the output node signals, are being “copied” to the output too, so as to be able to build a multivariate noise model. This approach has appeared to be very effective in handling confounding variables, e.g., in the single module identification problem.

Switching modules as a way to create identifiability

In dynamic networks identifiability conditions are typically satisfied by providing a sufficient number of external signals to the network. This can be either measured excitation signals or unmeasured disturbance signals. There is an alternative option for providing sufficient excitation in a network, by switching one or more modules between different dynamic settings. This situation has been laid down in a worked out method, for analyzing when switching modules provide sufficient excitation for network identifiability, see Dreef et al., IFAC SYSID 2021.

Case studies

Brain networks

In one case study, developed in cooperation with the team of neuroscientist Prof. Albert P. Aldenkamp, (SPS Group, Eindhoven University of Technology), our Bayesian method for estimating the topology of a dynamic network, was applied for inference of effective connectivity in brain networks for detecting the Mozart effect.
Several studies claim that listening to Mozart music affects cognition and can be used to treat neurological conditions like epilepsy. Research into this Mozart effect has not addressed how dynamic interactions between brain networks, i.e. effective connectivity, are affected.

In this study a new Bayesian topology estimation method is tested against the classical Granger-causality analysis and found to have favourable performance. Both methods have been used to infer the changes in effective interconnectivity in the brain network observed in fMRI data, in a group of subjects after intensively listening to Mozart’s sonata K448 at least 2 hours a day for 7 days. Here, we investigate if the effective connectivity of the subjects significantly changed after listening to Mozart music. The Bayesian method detected changes in effective connectivity between networks related to cognitive processing and control in the connection from the central executive to the superior sensori-motor network, in the connection from the posterior default mode to the fronto-parietal right network, and in the connection from the anterior default mode to the dorsal attention network. This last connection was only detected in a subgroup of subjects with a longer listening duration.
The results of this case study are published in R. van Esch et al. , Computers in Biology and Medicine, 2020.

Data-driven and model-based control in dynamic networks

Three main research lines have been explored, connecting data of an interconnected system to distributed controller design:

1. The identification of network models as a basis for distributed controller design;
2. Synthesizing a distributed controller directly on the basis of network data; and
3. Determining whether data are informativity for distributed controller design with stability and performance guarantees

In line 1) a distributed identification method has been presented based on an alternative information pattern where not all sensor data is available at one central location. In line 2), besides the development of a scalable distributed controller synthesis method,  methods have  been developed for distributed direct data-driven controller synthesis in a model-reference framework introducing virtual reference feedback tuning.  In line 3) two important contributions were made in specifying control performance guarantees for input-output data with cross-covariance bounds on the disturbances. The research results in this area have been collected in the PhD thesis of Tom Steentjes (2022).

SYSDYNET Matlab Toolbox

All methods for structural operations on network models have been collected in the SYSDYNET Matlab Toolbox. This Toolbox is under construction and  currently an alpha-testing version is available.
The toolbox has a graphical user interface for manipulating and performing operations on network structures, among which

• Parallel path and loop testing
• Immersion
• Canonical noise model construction
• Single module and full network identifiability test
• Allocation of external excitation signals and selection of measured nodes for guaranteeing identifiability
• Analysis and construction of predictor models for the local direct method

Graph-based methods for analyzing data-informativity

Scalable algorithms for single module identification